Как мы считаем
Введение.
Почему задачу нельзя решить руками.
Задача нахождения оптимального бюджета лечения является np-полной. Для решения задачи “в лоб”, требуется перебор всех возможных вариантов, что приводит к экспоненциальному росту сложности расчета при увеличении количества входных данных (группы пациентов и терапии). Например, только для одной нозологии меланома в предлагаемой платформой матрице расчета терапии 12 групп и 11 лекарств. Это значит, что количество возможных комбинаций
11 в 12 степени = 3 138 428 376 721 (три триллиона сто тридцать восемь миллиардов четыреста двадцать восемь миллионов триста семьдесят шесть тысяч семьсот двадцать один)
Одним из способов оптимизации расчета, является приведение условий к задаче линейного программирования, для решения которой можно использовать теорию оптимального распределения ресурсов лауреата нобелевской премии по экономике Л.В. Канторовича.
Решение
Условия задачи
- Мы не должны превышать заданный бюджет
- Эффективность лечения должна быть максимальной
- Для каждой группы может быть применена только одна терапия
Входные данные:
- Массив терапий (цена, эффективность)
- Массив групп пациентов (количество пациентов, выживаемость, доступные терапии)
В ответ получаем бюджет, выживаемость, массив решений (группа, терапия)
Формулировка задачи:
Условия:
Назначение одной терапии каждой группе
Бюджетное ограничение
Ограничение на разрешенные типы терапии
Переменные:
— номер группы
— номер терапии
— количество пациентов в i-ой группе
— успешность лечения (например, выживаемость в течение определенного срока) пациентов в i-ой группе
— успешность (например, выживаемость в течение определенного срока) лечения j-ой терапии
— факт применения j-ой терапии для i-ой группы
— факт доступности j-ой терапии для i-ой группы
— количество пациентов во всех группах
Для вычисления результатов, используем метод комбинаторной оптимизации задач линейного программирования Ветвление и отсечение.
Блок-схема алгоритма расчета
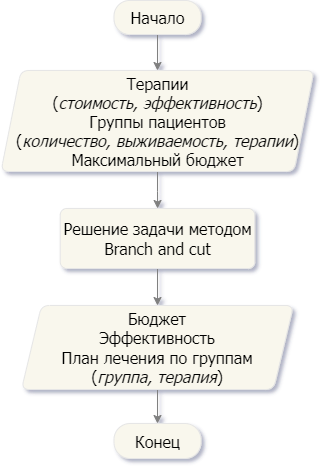
Валидация модели
Приведем сравнение решения задачи нахождения оптимального плана лечения способом полного перебора и оптимизированного алгоритма системы. Для повышения наглядности примера, упростим исходные данные до трех групп пациентов и двух лекарственных средств для каждой группы.
Лекарственные средства
| Наименование | Стоимость | Успешность лечения |
|---|---|---|
| (1) Capecitabine | 5 746,00 | 45% |
| (2) Capecitabine+bevacizumab | 26 046,00 | 60% |
| (3) XELOX | 10 566,00 | 70% |
| (4) FOLFIRI+cetuximab | 88 497,00 | 82% |
| (5) FOLFOX+bevacizumab | 21 345,00 | 33% |
| (6) FOLFOXIRI+bevacizumab | 29 954,00 | 41% |
Группы пациентов
| Группа | Количество пациентов | Успешность лечения, % | Лекарственное средство |
|---|---|---|---|
| A (РТК, ободочная кишка, тип I-IIA) | 25 | 82% | 1. Capecitabine 2. Capecitabine+bevacizumab |
| B (РТК, ободочная кишка, тип IIB-III) | 15 | 74% | 3. XELOX 4. FOLFOX+cetuximab |
| C (РТК, ободочная кишка, тип IV) | 7 | 80% | 5. FOLFOX+bevacizumab 6. FOLFOXIRI+bevacizumab |
Расчет полным перебором
Для полного перебора всех вариантов планов лечения трех групп пациентов одним из двух лекарственных средств (для каждого), потребуется вычислить 23 = 8 вариантов и выбрать вариант с наилучшей успешностью, укладывающееся в бюджетный лимит.
Вариант I
| Группа | Лекарственное средство | Успешность лечения | Стоимость |
|---|---|---|---|
| A | 1 | 82% * 45% = 36,9% | 25 * 5746 = 143 650,00 |
| B | 3 | 74% * 70% = 51,8% | 15 * 10566 = 158 490,00 |
| C | 5 | 80% * 33% = 26,4% | 7 * 21345 = 149 415,00 |
| Итого | 40,04% | 451 555,00 |
Вариант II
| Группа | Лекарственное средство | Успешность лечения | Стоимость |
|---|---|---|---|
| A | 2 | 82% * 60% = 49,2% | 25 * 26046 = 651 150,00 |
| B | 3 | 74% * 70% = 51,8% | 15 * 10566 = 158 490,00 |
| C | 5 | 80% * 33% = 26,4% | 7 * 21345 = 149 415,00 |
| Итого | 46,59% | 959 055,00 |
Вариант III
| Группа | Лекарственное средство | Успешность лечения | Стоимость |
|---|---|---|---|
| A | 1 | 82% * 45% = 36,9% | 25 * 5746 = 143 650,00 |
| B | 4 | 74% * 82% = 60,68% | 15 * 88497 = 1 327 455,00 |
| C | 5 | 80% * 33% = 26,4% | 7 * 21345 = 149 415,00 |
| Итого | 42,88% | 1 620 520,00 |
Вариант IV
| Группа | Лекарственное средство | Успешность лечения | Стоимость |
|---|---|---|---|
| A | 1 | 82% * 45% = 36,9% | 25 * 5746 = 143 650,00 |
| B | 3 | 74% * 70% = 51,8% | 15 * 10566 = 158 490,00 |
| C | 6 | 80% * 41% = 32,80% | 7 * 29954 = 209 678,00 |
| Итого | 41,04% | 511 818,00 |
Вариант V
| Группа | Лекарственное средство | Успешность лечения | Стоимость |
|---|---|---|---|
| A | 2 | 82% * 60% = 49,2% | 25 * 26046 = 651 150,00 |
| B | 4 | 74% * 82% = 60,68% | 15 * 88497 = 1 327 455,00 |
| C | 5 | 80% * 33% = 26,4% | 7 * 21345 = 149 415,00 |
| Итого | 49,42% | 2 128 020,00 |
Вариант VI
| Группа | Лекарственное средство | Успешность лечения | Стоимость |
|---|---|---|---|
| A | 2 | 82% * 60% = 49,2% | 25 * 26046 = 651 150,00 |
| B | 3 | 74% * 70% = 51,8% | 15 * 10566 = 158 490,00 |
| C | 6 | 80% * 41% = 32,80% | 7 * 29954 = 209 678,00 |
| Итого | 47,59% | 1 019 318,00 |
Вариант VII
| Группа | Лекарственное средство | Успешность лечения | Стоимость |
|---|---|---|---|
| A | 1 | 82% * 45% = 36,9% | 25 * 5746 = 143 650,00 |
| B | 4 | 74% * 82% = 60,68% | 15 * 88497 = 1 327 455,00 |
| C | 6 | 80% * 41% = 32,80% | 7 * 29954 = 209 678,00 |
| Итого | 43,88% | 1 680 783,00 |
Вариант VIII
| Группа | Лекарственное средство | Успешность лечения | Стоимость |
|---|---|---|---|
| A | 2 | 82% * 60% = 49,2% | 25 * 26046 = 651 150,00 |
| B | 4 | 74% * 82% = 60,68% | 15 * 88497 = 1 327 455,00 |
| C | 6 | 80% * 41% = 32,80% | 7 * 29954 = 209 678,00 |
| Итого | 50,42% | 2 188 283,00 |
Результаты с помощью полного перебора
В рамки бюджетного ограничения укладываются следующие варианты:
| Вариант | Успешность | Стоимость |
|---|---|---|
| I | 40,04% | 451 555,00 |
| II | 46,59% | 959 055,00 |
| IV | 41,04% | 511 818,00 |
Очевидно, что план лечения, рассчитанный в варианте II, обеспечивает наибольшую успешность лечения с бюджетом до 1 000 000.
Результаты с помощью алгоритма
| Группа | Количество пациентов | Лекарственное средство | Успешность лечения, % | Стоимость |
|---|---|---|---|---|
| РТК, ободочная кишка, тип I-IIA | 25 | Capecitabine+bevacizumab | 49,20 | 651 150,00 |
| РТК, ободочная кишка, тип IIB-III | 15 | XELOX | 51,80 | 158 490,00 |
| РТК, ободочная кишка, тип IV | 7 | FOLFOX+bevacizumab | 26,08 | 149 415,00 |
| Итого | 47 | 46,59% | 959 055,00 |
Выводы
Оптимизированный, при помощи методов линейного программирования, алгоритм расчета дает результат идентичный расчету полным перебором. В то время, как сложность расчета полным перебором имеет экспоненциальный рост сложности с ростом объема входных данных, оптимизированный алгоритм позволяет выполнять расчеты с большим количеством входных данных с использованием значительно меньших ресурсов.